Real Numbers
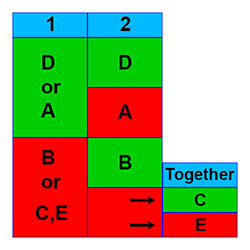
Every Data Sufficiency (DS) question can have 1 of 5 possible answers, and the possible answers are the same for every DS question. All DS questions are really two questions in one. You’re given a general problem, followed by two supplemental statements. The real problem is to evaluate each of the two statements independently to determine their individual sufficiency to solve the original general problem. As you determine the sufficiency of these statements, you are able to decide which of the following 5 answers to the Data Sufficiency question is the correct answer:
A. Statement 1 is sufficient, but statement 2 is not.
B. Statement 1 is not sufficient, but statement 2 is.
C. Neither statement 1 nor statement 2 is sufficient, but together they are.
D. Both statement 1 and statement 2 are individually sufficient.
E. Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
The diagram above gives a pictorial representation of the 5 Data Sufficiency answers. The two statement numbers are shown in blue at the top of the first two columns. Note that green means sufficient, and red means not sufficient. As an example, if both statements 1 and 2 are individually sufficient, then the correct answer is D. For more information on the 5 DS answers, see our videos.
We illustrate these answers for real number problems with the following 5 examples. Each of the first two examples provides 5 different versions of supplementary statements for the same general problem, and each of these 5 versions yields a different one of the 5 possible answers. The answers to these 5 versions are explained immediately after the problem. After the first 2 examples, we then give 3 additional examples with just one version of the supplementary statements.
[Notice in the first 2 examples that the 5 versions of the supplementary statements provide examples of the 5 different answers, A – E. However, they are not given in A – E order.]
Example 1)
s and g are distinct, positive real numbers. What is the ratio of g to |s – g|?
Version I.
(1) |s – g| = s – g
(2) 1/z = 1/(s – g)
Version II.
(1) 2/(3g) = 1/(s – g)
(2) |s – g| = s – g
Version III.
(1) |s – g| = s – g and 1/z = 1/(s – g)
(2) 2z = 5g
Version IV.
(1) Double s is the same as five times g.
(2) 2/(3g) = 1/(s – g)
Version V.
(1) 1/z = 1/(s – g)
(2) Double s is the same as five times g.
Answers: [ Version I: E Version II: A Version III: C Version IV: D Version V: B ]
Explanation:
Version I: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) |s – g| = s – g
Partial information. This only tells us g < s, but doesn’t give us any information about their comparative sizes. Not sufficient.
(2) 1/z = 1/(s – g)
Partial information. This introduces a new variable, z, without giving us any new information about s and g. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because they give us no information about the comparative sizes of s and g.
Version II: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) 2/(3g) = 1/(s – g)
Full information. This equation can be transformed to 2 = 3g/(s – g), and finally, 2/3 = g/(s – g). Since g is positive and this ratio (2/3) is positive, s – g is positive, so |s – g| = s – g. Sufficient.
(2) |s – g| = s – g
Partial information. This only tells us g < s, but doesn’t give us any information about their comparative sizes. Not sufficient.
Version III: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) |s – g| = s – g and 1/z = 1/(s – g)
Partial information. This tells us g < s, and introduces a new variable, z, which is equal to s – g, but doesn’t give us any information about their comparative sizes. Not sufficient.
(2) 2z = 3g
Partial information. This introduces a new variable, z, and gives us comparative information about z with g, but tells us nothing about the comparative sizes of s and g. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because statement 1 tells us that, inverting both sides of the equation, z = s – g. Knowing this, we can use statement 2 to determine that 2(s – g) = 3g, so 2/3 = g/(s – g).
Version IV: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) Double s is the same as five times g.
Full information. This says that 2s = 5g, so g < s, and |s – g| = s – g. 2s = 5g also implies this series of equations:
s = (5/2)∙g
s – g = (5/2)∙g – g
s – g = (3/2)∙g
2/3(s – g) = g
2/3 = g/(s – g)
So the ratio of g to |s – g| is 2/3. Sufficient.
(2) 2/(3g) = 1/(s – g)
Full information. This equation can be transformed to 2 = 3g/(s – g), and finally, 2/3 = g/(s – g). Since g is positive and this ratio (2/3) is positive, s – g is positive, so |s – g| = s – g. Sufficient.
Version V: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) 1/z = 1/(s – g)
Partial information. This introduces a new variable, z, without giving us any new information about s and g. Not sufficient.
(2) Double s is the same as five times g.
Full information. This says that 2s = 5g, so g < s, and |s – g| = s – g. 2s = 5g also implies this series of equations:
s = (5/2)∙g
s – g = (5/2)∙g – g
s – g = (3/2)∙g
2/3(s – g) = g
2/3 = g/(s – g)
So the ratio of g to |s – g| is 2/3. Sufficient.
To practice more of these types of problems, click here.
Example 2)
a, b, c, and d are non-zero real numbers such that a < b < c < d. Which of these has the smallest absolute value?
Version I.
(1) c = -a
(2) b < 0 and c + b > 0
Version II.
(1) d + b < c
(2) c + b > 0
Version III.
(1) c = -a
(2) d + b < c
Version IV.
(1) d + b > a + d
(2) b < 0 and c + b > 0
Version V.
(1) d + b < c
(2) d + b > a + d
Answers: [ Version I: D Version II: C Version III: A Version IV: B Version V: E ]
Explanation:
Absolute value is a measure of closeness to 0. The lower the absolute value of a number, the closer it is to 0. For this problem, we start off knowing a, b, c, and d are arranged in ascending order. This is important information that needs to be remembered with each additional piece of information. Specifically, if a is positive, then its absolute value is the smallest. But if b is negative, then its absolute value must be less than that of a.
Version I: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) c = -a
Full information. This looks confusing, because it appears that it’s saying c is a negative number. But if we multiply both sides by -1, we get –c = a, and now, since a < c, we know that a is negative, and c is positive. But if –c = a, then their absolute values are equal. Since b is between a and c, it must be closer to 0 than both a and c, and therefore have a smaller absolute value than they do. Since d is positive and larger than c, its absolute value is the largest. So b is the answer. Sufficient.
(2) b < 0 and c + b > 0
Full information. The first half tells us that b is negative, and the second half that c is positive but its absolute value is larger than that of b. Since b is negative and larger than a, its absolute value is also less than that of a. And since c is positive, and less than d, then the absolute value of d is larger than that of both b and c. Sufficient.
Version II: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) d + b < c
Partial information. This only tells us that b is negative. Its absolute value could still be much larger than either d or c, or it could be smaller than both. Not sufficient.
(2) c + b > 0
Partial information. This tells us that c is positive, but b could be either positive or negative. If b were positive, this statement would be true, and if it were negative the statement could be true. In both cases the absolute value of b would be smaller than that of c and d. But the statement tells us nothing about the absolute value of a. If b is positive, then the absolute value of a could be smaller than that of b, c, and d, but it could also be larger. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because since statement 1 tells us that b is negative, then its absolute value is smaller than that of a. Statement 2 tells us that the absolute value of b is less than that of c, and of course it would also be less than that of d.
Version III: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) c = -a
Full information. This looks confusing, because it appears that it’s saying c is a negative number. But if we multiply both sides by -1, we get –c = a, and now, since a < c, we know that a is negative, and c is positive. But if –c = a, then their absolute values are equal. Since b is between a and c, it must be closer to 0 than both a and c, and therefore have a smaller absolute value than they do. Since d is positive and larger than c, its absolute value is the largest. So b is the answer. Sufficient.
(2) d + b < c
Partial information. This only tells us that b is negative. Its absolute value could still be much larger than that of either d or c, or it could be smaller than both. Not sufficient.
Version IV: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) d + b > a + d
No information. We already knew this, since a < b. Not sufficient.
(2) b < 0 and c + b > 0
Full information. The first half tells us that b is negative, and the second half that c is positive but its absolute value is larger than that of b. Since b is negative and larger than a, its absolute value is also less than that of a. And since c is positive, and less than d, then the absolute value of d is larger than that of both b and c. Sufficient.
Version V: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) d + b < c
Partial information. This only tells us that b is negative. Its absolute value could still be much larger than either d or c, or it could be smaller than both. Not sufficient.
(2) d + b > a + d
No information. We already knew this, since a < b. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because statement 1 is insufficient, and statement 2 gives us no new information.
To practice more of these types of problems, click here.
Example 3)
Is mn ≤ 1?
(1) 0 ≤ m ≤ 10 and -10 ≤ n ≤ 10
(2) 0 ≤ m ≤ 10 and -10 ≤ n ≤ 0
Answer: B – Statement 1 is not sufficient, but statement 2 is.
Explanation:
(1) 0 ≤ m ≤ 10 and -10 ≤ n ≤ 10
Partial information. If n is negative or 0, then mn is negative or 0, and this will be less than 1. However, if n is 1 and m is 10, their product is 10 which is greater than 1. Thus, the information here is inconclusive. Not sufficient.
(2) 0 ≤ m ≤ 10 and -10 ≤ n ≤ 0
Full information. If m is positive and n is negative, then their product is negative, and this will be less than 1. If either is 0, their product is 0, and this is less than 1. Sufficient.
Example 4)
If x is any real number, then the greatest integer of x, [x], is the largest integer which is less than or equal to x. Suppose x has at least 2 places, but not an infinite number of places, to the right of the decimal point. Then what are the tenths and hundredths digits of x?
(1) [x] = [x + .01], but [x] < [x + .02]
(2) [x + .01] < [x + .02]
Answer: D – Both statement 1 and statement 2 are individually sufficient.
Explanation:
(1) [x] = [x + .01], but [x] < [x + .02]
Full information. If [x] = [x + .01], then we know that the decimal portion of x must be less than .99, but if [x] < [x + .02], it is not less than .98. Thus, the tenths and hundredths digits are 9 and 8. Sufficient.
(2) [x + .01] < [x + .02]
Full information. A decimal value of .99 does not satisfy this relation, nor does any decimal value less than .98. .98 is the only 2 digit decimal value that does. Thus, the digits must be 9 and 8. Sufficient.
Example 5)
For integers a and b, is \(\begin{align}a^2 + b^3\end{align}\) negative?
(1) b < 0
(2) |b| > |a|
Answer: C – Neither statement 1 nor statement 2 is sufficient, but together they are.
Explanation:
It doesn’t matter whether a is a positive or negative integer, \(\begin{align}a^2\end{align}\) will always be positive. If b is positive, then \(\begin{align}b^3\end{align}\) is positive, but if b is negative, then \(\begin{align}b^3\end{align}\) will be negative. If b is negative, and its absolute value, |b|, is greater than the absolute value of a, |b| > |a|, then \(\begin{align}a^2 + b^3\end{align}\) will be negative. However, it’s also possible for b to have a smaller absolute value than a, but for \(\begin{align}a^2 + b^3\end{align}\) to still be negative. This will happen if b is negative, and the absolute value of \(\begin{align}b^3\end{align}\) is greater than the absolute value of \(\begin{align}a^2\end{align}\). We see this, for example, when a = -4 and b = -3. In this case, \(\begin{align}a^2 + b^3\end{align}\) = 16 – 27 = -11.
(1) b < 0
Partial information. This gives us a little helpful information, because we now know that \(\begin{align}b^3\end{align}\) is negative, but without a relationship of b to a, we can’t decide whether or not \(\begin{align}a^2 + b^3\end{align}\) is negative. Not sufficient.
(2) |b| > |a|
Partial information. This is helpful, but if both a and b are positive, then \(\begin{align}a^2 + b^3\end{align}\) will be positive. If we knew b were less than 0, we could answer the question. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because knowing that b is less than 0, and knowing that its absolute value is greater than that of a, we know that \(\begin{align}a^2 + b^3\end{align}\) is negative.
To practice more of these types of problems, click here.